stars

This is a topic from a loong time ago. I was in highschool, one morning while having breakfast I started doodling some stars on the table.

You can draw these stars connecting their points with straight lines. So I asked the only reasonable question you can ask yourself at six thirty in the morning…

How far can I take this?

stars and little numbers

Let’s start with some assumptions. Let’s say that we can start with any number of vertices equally distributed on a circle, the vertices of any regular polygon if you prefer. Let’s experiment with n = 5.

Then let’s try to build the standard star, to do so let’s choose a vertex and see what we need to do. I prefer to draw clockwise, but it’s arbitrary.

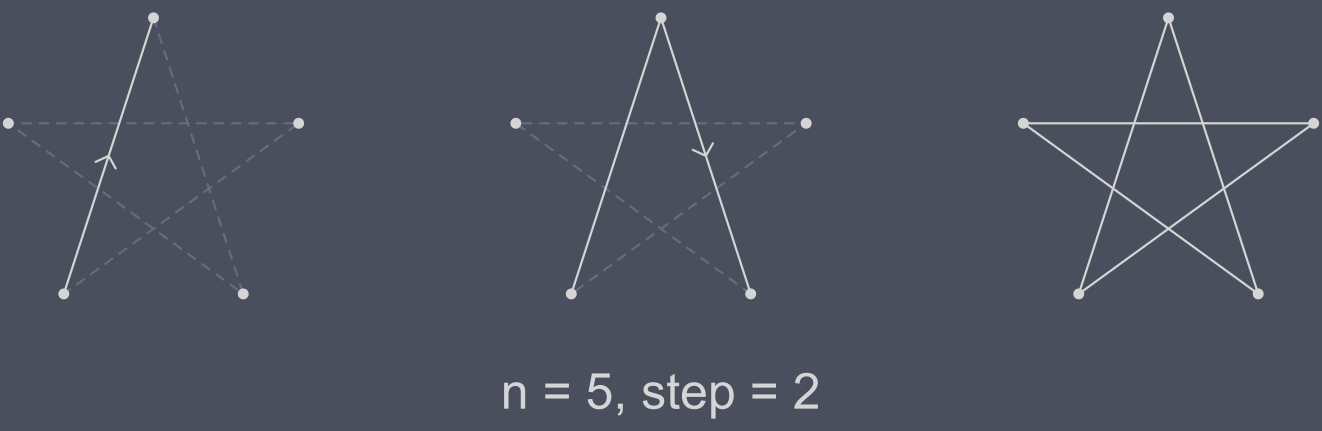
Now we see that we are connecting a vertex with the vertex at distance two (or skipping one if you prefer), I will say that we use step = 2.

What happens if we change the step?

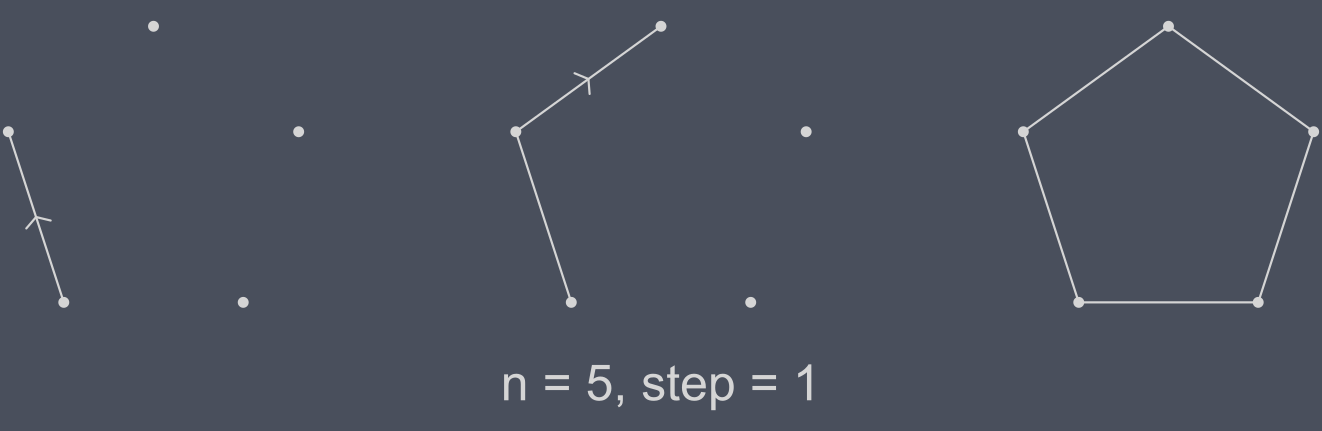
Well, with step = 1 we are simply drawing our regular polygon, which makes sense, we are following the outside shape.

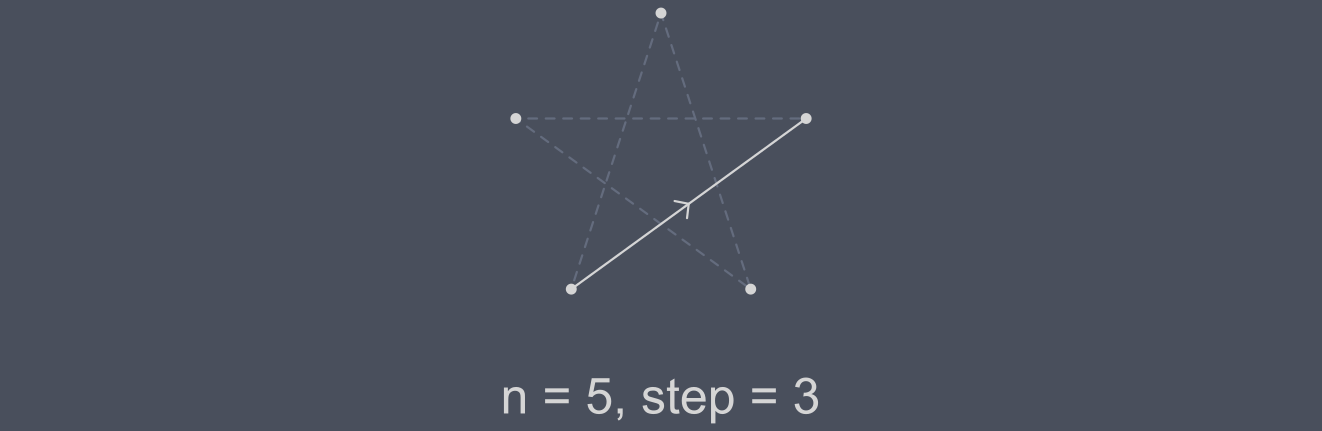
With step = 3 we are drawing our original star, but moving anticlockwise. This happens because 3 is bigger than the half of our n, so we are moving backwards, as if step was -2.

It seems that we have exhausted all the possibilities…

But let’s keep playing, we can always change n, we are not limited to pentagons.

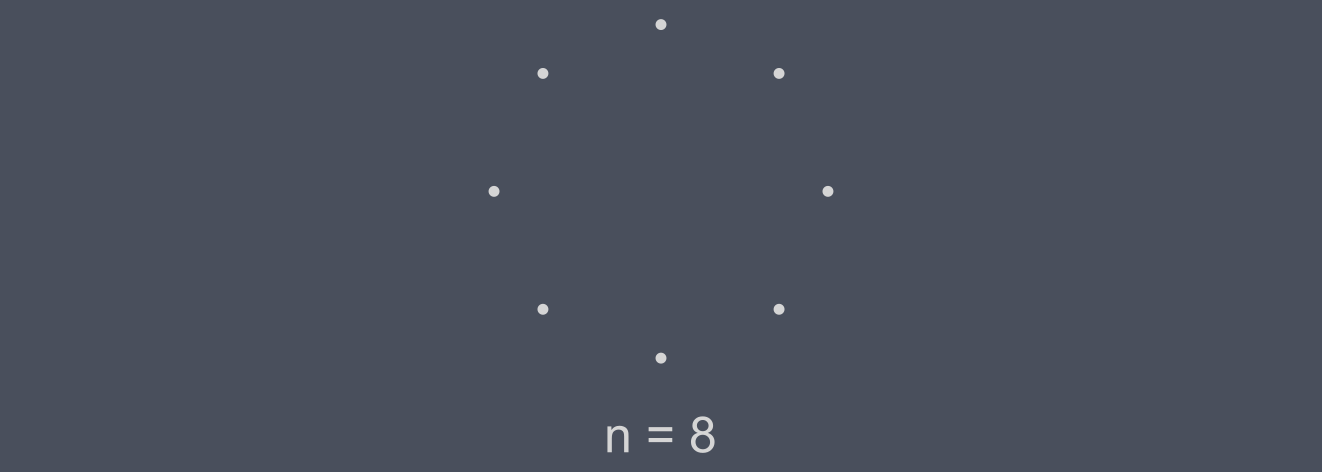
With a nice octagon we have way more steps to try, let’s see firstly if what we learned before is still true.

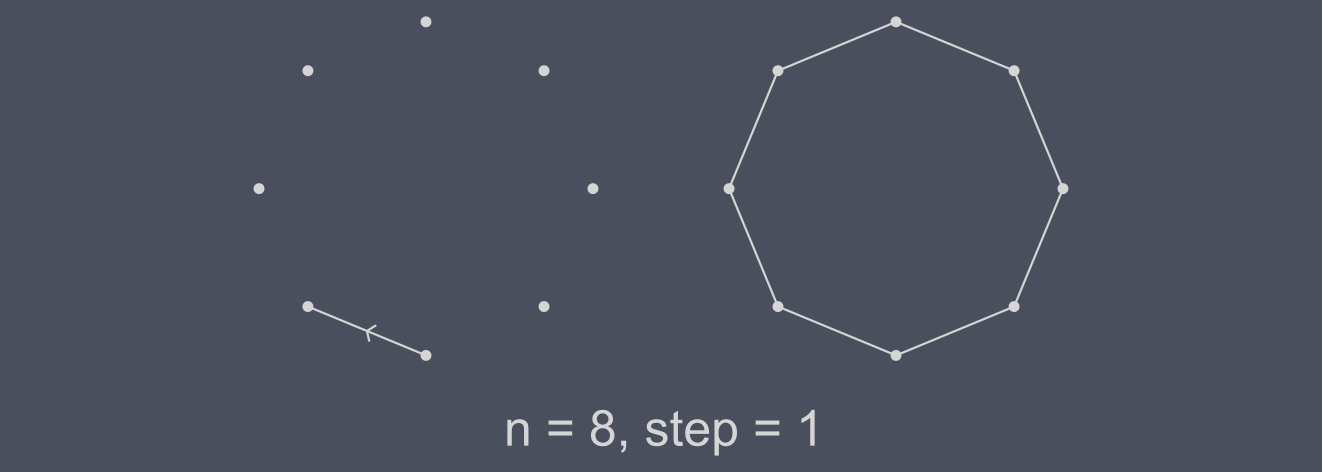
Yep, we are drawing the octagon ahah

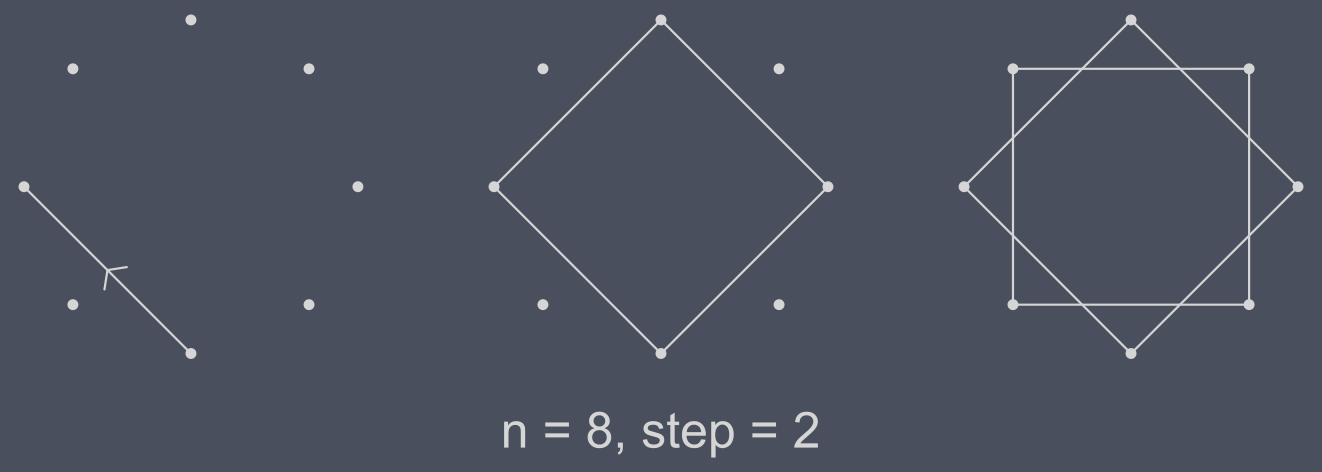
Mmmmhhh, to complete this star we had to introduce another rule. Since our number of steps is a divisor of n (actually it happens if step and n are not coprime integers), we found ourselves at the starting vertex without having explored all of them. To solve this, we can ideally pick up our pencil and start again from one of the vertices we haven’t met yet. Doing so will gives us a nice results. In this case we ended up with two squares. The fact that n = 8, step = 2 is equal to n = 4, step = 1 (a square) twice feels nice :)

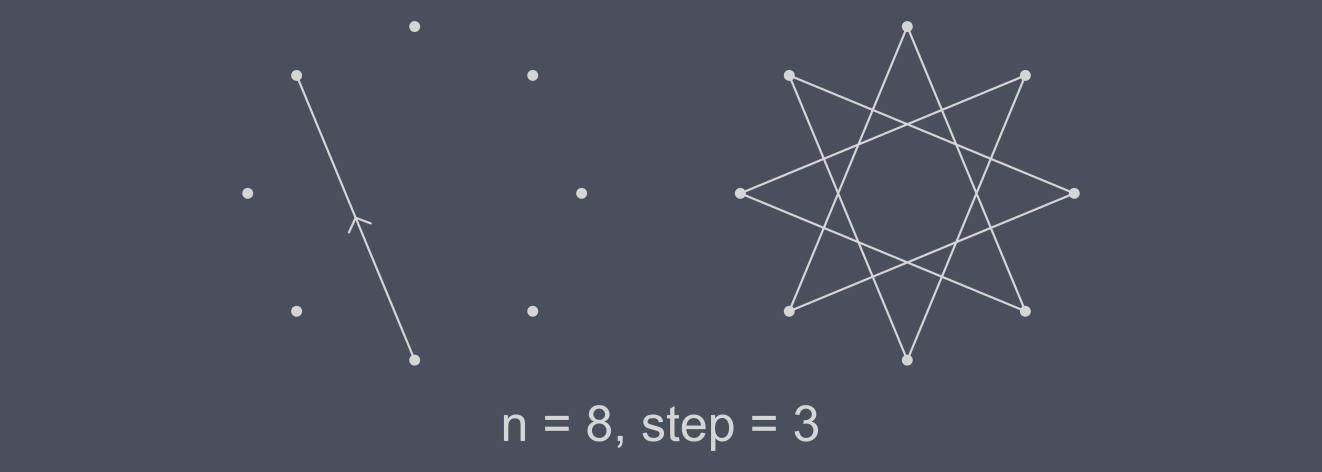
This is one of my favourite stars. I saw it when I was a kid as a decoration in a medieval castle and I remember being so captivated by it that I had to learn the pattern even before understanding how it made sense in the bigger context. That morning during breakfast I was actually doodling this star when I started thinking about all of this.

Let’s continue!

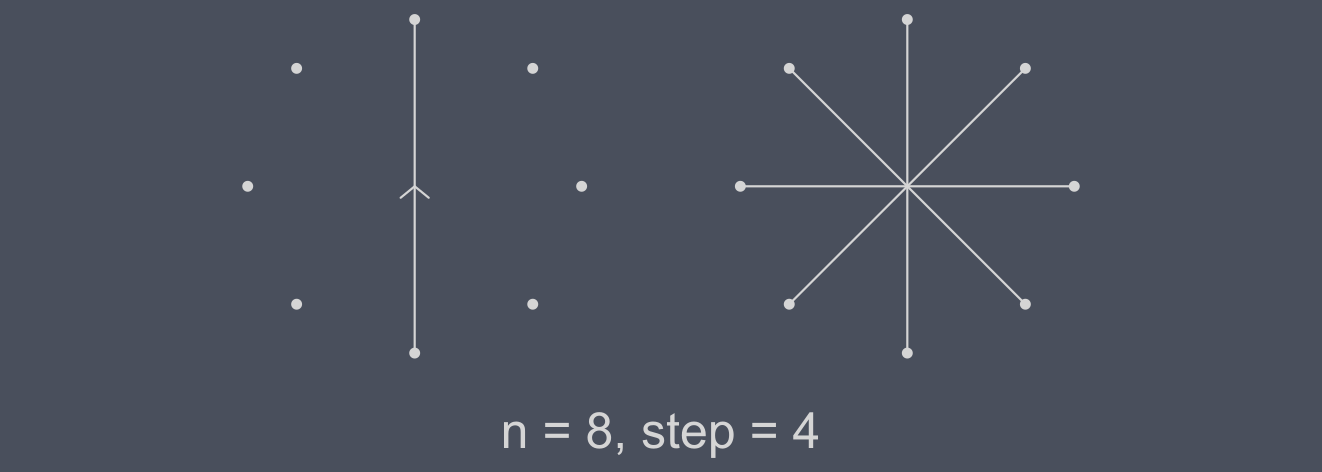
Ok, this is kinda of a downgrade, but in the end we would get this for all the even-pointed stars if the step is half of n. We need to repeat the step of choosing another starting point three times, but in the end we still get a star.

final remarks

Now, these are the basic rules, now you can go around and draw stars!

Just some observations…

A star drawn with any step will contain smaller versions with the same number of vertices, but smaller steps. To observe this phenomenon we need relatively bigger n, but even our standar star (n = 5, step = 2) contains a little pentagon (n = 5, step = 1). Drawing them by hands makes it more and more difficult to see clearly the little versions with higher n.

Another way to look at this feature is imagining to start with the poligon and extending the sides until they meet the extensions of the others (this idea was given to me by a friend). At the beginning the sides at distance two will meet (step = 2) and then the others.

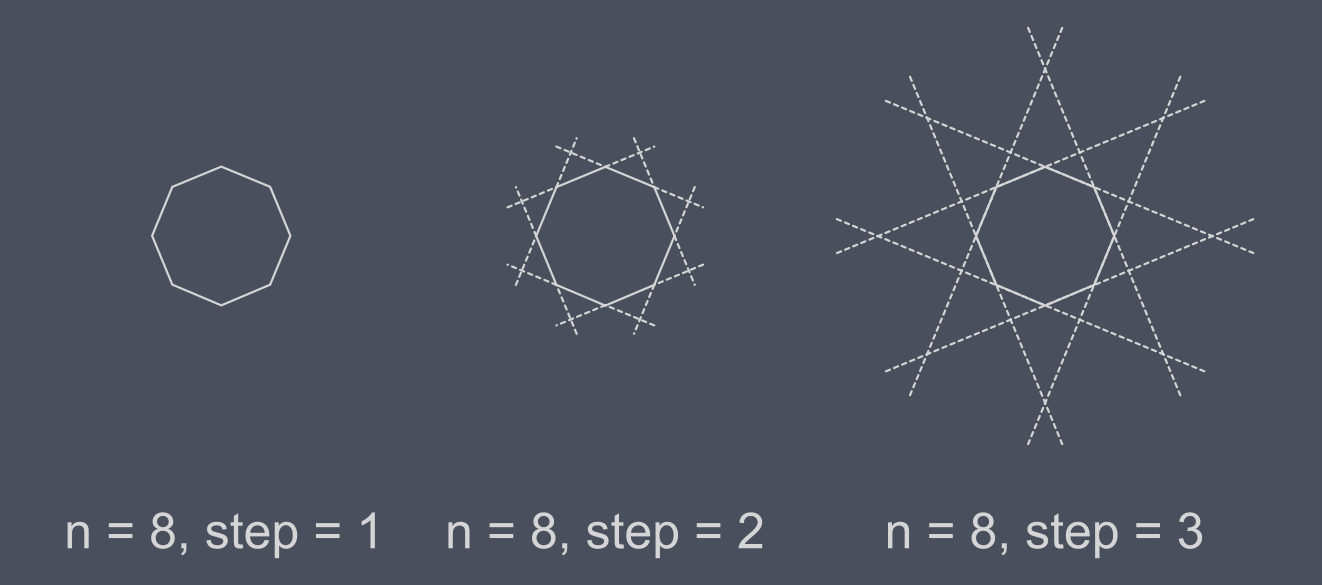
It’s impossible to obtain the version made of sticks (n even, step = n/2) by any of this methods, but we can imagine that we are looking at our star from infinite distance or that we are extending our sides in the infinite, where even parallel lines can meet.

Just to say goodbye, here some other cool stars :)

Have fun and draw some stuff!!